This question was posed to me, and I was surprised that I could not find a solution (as I thought that all rook tours [open or closed] were possible). Starting from a8, could a rook visit every square on the board once, ending on f3?
I tried a few times, with a few different strategies, but I always ended up missing one square.
It’s really easy to burn pairs of rows or columns, so the problem space could be reduced…
…but at some point (4x4), I was able to convince myself that it is impossible (at least at this size and state):
…but it might be possible that shaving off column or row pairs is also discarding a solution?
You must log in or register to comment.
Any route from white to white visiting N white squares must visit exactly N-1 black squares. Any route from white to black visiting N white squares must visit exactly N black squares. Therefore on a board with an equal amount of white and black squares, it’s not possible to walk a route from a white square to a white square and visit all squares.
You can prove it through induction. Starting with a route that visits just one white square, you visit zero black squares. Then, if you want to extend your route with one white square, you must also visit exactly one black square to get to it, as no two white squares border one another. Meaning for a route of S steps (where each ‘step’ is actually two moves from a white square to the next white square), you visit S+1 white squares and S black squares, or equivalently N white squares and N-1 black squares.
All the grids have even number of squares (equal black and white). Therefore it is impossible to start on white and end on white while covering everything else.
I don’t have the formal proof for this, but can be proven with examples. In each of your grids.
I’ll be following this thread to see if someone shares the formal proof for this, fingers crossed!
You’re right, guess the reason is that the rook changes the colour of the square it’s on with every move. After an odd number of moves it’s on the opposite colour, after an even number of moves it’s back on the colour it started on. So, no sequence of 63 moves starting on a light square can ever end on another light square.
This puzzle is definitely impossible. In fact it seems to be some sort of parity issue, although I’m having trouble with the actual proof. Basically if you always keep the start in the top left corner, then you can only complete a rook’s tour if the end square has an odd manhattan distance (x distance + y distance). If you put the end square an even manhattan distance away, then you create this issue where you’re always unable to hit one square.
For example, even parity, impossible:
Odd parity, possible:
You start in white and you can only move to black. Then you have to move to white again then black, then white, then black and so on. For a sequence with an even number of terms you have to end on black if you start in white .Since the puzzle states you have to start and end on white it’s impossible.
Uhhhh yeah?
I found this to be really easy but I don’t play chess so maybe I’m misunderstanding or perhaps the question was worded wrong?
Using these rules from your post
“Starting from a8, could a rook visit every square on the board once, ending on f3?”
And standard rook movement
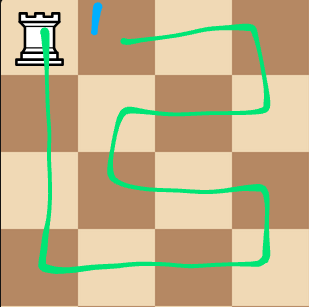
I came up with this solution.
Follow the numbers up or down from the start or finish. Highlighted squares show moves to squares that aren’t adjacent.
I’d imagine there’s lots of solutions with different patterns, this is just the one that came to me on the fly.
The rule is better said that you can visit each square “once and only once.” Every time you move to a non-adjacent square, you’re crossing a square for a second time and breaking the rule.
If you can only move to black squares from white squares then for a sequence with an even number of terms if you start on a white square you have to end on a black square. Because the problem states you have to start and end on white it’s impossible to do without crossing over squares.
Did you start from the square labeled “end”?
Don’t think of it as the number being the order of the steps, think of it as being how many are left lol
The other puzzles in your post are also solvable btw but I won’t spoil them
doesn’t visit usually mean “ends movement in that square”? 'Cause that means skipping squares is allowed. So just fill out the board until the last row and skip ahead of the end tile while doing so. Do the last row in an order that the last col is the same col as the end square, move to end square.
deleted by creator
… unless I don’t fully understand the problem.
Diagonal move in top right corner?
Edit: wait actually along the whole right side
Thanks for pointing that out. That mistake was easily mendable.
I hope I haven’t blundered somewhere else.
In this context, you cannot cross a square without visiting it.
Logical proof of why it’s not possible for your given rules of not being able to pass through squares.
You start in white and you can only move to black. Then you have to move to white again, then black, then white, then black and so on. For a sequence with an even number of terms you have to end on black if you start in white .Since the puzzle states you have to start and end on white it’s impossible.
I don’t think it’s possible in that case
Mmm that’s a good way of showing it, very visual and easy to follow.
Rooks don’t move diagonal. I was able to do this exercise in my head on about the third try however. Start with big laps round the outside x2, then column by column to finish
I may not be understanding you correctly. Can you elaborate? Feel free to use coordinates.
I am afraid that I didn’t apply any rigor here and thought I solved it. Been playing with it for a bit and see there is likely not a solution. Good fun for me.
Seems this is related to Hamiltonian path problems. The issue is there is always one square that can’t be picked up. Why could this be?
So the rook has to move from a white square to a black square or a black square to a white one. This would mean the sequence would go white, black, white, black and so on for all squares. Since there is an even number of squares if the rook starts on white it must end on black but the problem states the start and end squares are both white, thus impossible to solve. Doesn’t really have anything to do with hamiltonian paths because they are loops that will fill a space. It does relate more broadly to space filling curves in general but I think a graphical approach to this problem can be a bit misleading.
Interestingly you can pick any two white squares on the chess board and you couldn’t make a path between them in the way op is trying to.
If you take the rooks movement, and reduce each longer move to a series of single steps a1a2a3a4 for example, this becomes a Hamiltonian problem. The corners have 2 nodes, the edges three, and the core has four. Black and white indicates even or uneven distance in nodes.
Ahh yes sorry my bad I mixed up hamiltonian and hilbert in my head
The 2x2 case is impossible, I suspect it is related in some way.
You’re forgetting knook promotion when you reach the opposite side, combining the knight and rook tour, making it possible again
